記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。
還不了解，內容可能有錯誤。

之前有紀錄排序的程式來源 ，現在學習排序的一些觀念
java，quicksort、Counting Sort和c++ ，mergesort、Heap Sort和 js ，Shell Sort、Radix Sort
https://ithelp.ithome.com.tw/articles/10219345

[演算法] 排序演算法(Sort Algorithm)
http://notepad.yehyeh.net/Content/Algorithm/Sort/Sort.php

堆積排序法(Heap Sort)

堆積排序法(Heap Sort) 分為兩種:

最小堆積(Min Heap)：父節點的值 < 子節點的值
Root 會是最小值 。

最大堆積(Max Heap)：父節點的值 > 子節點的值。
Root 會是最大值

Max Heap 排序方法 :

步驟 1 : 
將Complete Binary Tree 的 陣列 轉成 Max Heap 。

步驟2 : 
因為 root 是最大值 ，所以Max Heap 排序 ，就是不斷把root拿出來。

把root拿出來的方法 : 把root 和 最後一個節點(陣列最後一項) 交換 。

所以 最後面 就會是 數列的最大值 。

但交換後 ，Max Heap  又會亂掉 ， 所以把 剩餘陣列 轉成 Max Heap (忽略最後一項，因為不斷把root 丟到最後面 ，後面數列會是排序好的結果，所以忽略) 。

總結:
建Max Heap
去root
建Max Heap
去root
建Max Heap
去root

次數: 陣列個數-1

Min Heap 排序方法 :

步驟 1 : 
將Complete Binary Tree 的 陣列 轉成 Min Heap 。

步驟2 : 
因為 root 是最小值 ，所以Min Heap 排序 ，就是不斷把root拿出來。

把root拿出來的方法 : 把root 和 最後一個節點(陣列最後一項) 交換 。

所以 最後面 就會是 數列的最小值 。

但交換後 ，Min Heap  又會亂掉 ， 所以把 剩餘陣列 轉成 Min Heap (忽略最後一項，因為不斷把root 丟到最後面 ，後面數列會是排序好的結果，所以忽略) 。

總結:
建Min Heap
去root
建Min Heap
去root
建Min Heap
去root
次數: 陣列個數- 1

Min Heap排序 、Max Heap排序 不同的地方在哪 ?

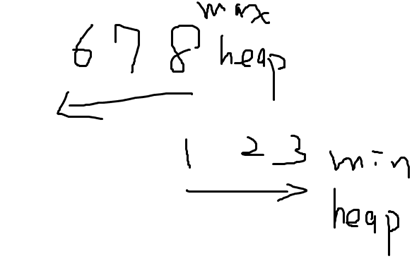
Max heap 可以從陣列最後面 依序 放最大值:
n ，n-1， n-2

Min heap 只能把每次的 最小值 放到第 n 個位置 ，這樣最後才會是從小到大 。

所以Min heap 如果沒特別改變寫法的話 ，root從n ，n-1， n-2 這樣放的話，
排序 會是由大到小 。

來看程式:
HeapSort
https://www.geeksforgeeks.org/heap-sort/
Heap Sort | GeeksforGeeks
https://www.youtube.com/watch?v=MtQL_ll5KhQ&ab_channel=GeeksforGeeks

程式大概都是 : MaxHeap 的 sort 從小到大 。

建立heap的function 通常取名為 Heapify( Heapify 是指每一步驟，不過先這樣記吧) :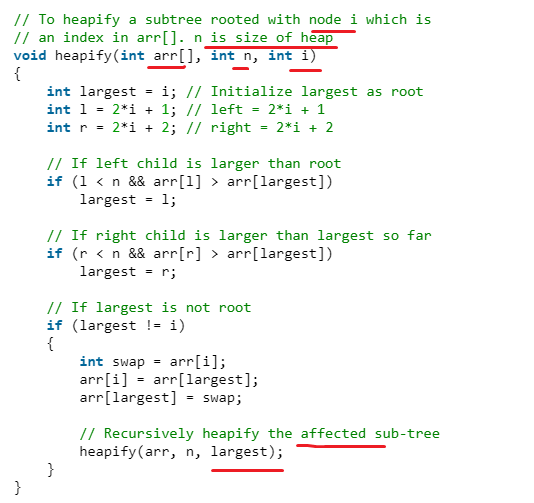

heapify有3個參數

    void heapify(int arr[], int n, int i) {

    }
arr[] 就是陣列 ，整個數列 。
n 是 MaxHeap的 個數 ，因為會不斷地把最大值往右搬 ， 所以MaxHeap的 個數 會不斷-1-1
i 是要調整的節點(陣列的索引值) 。

heapify方法裡的內容 :

i 是現在想調整的節點
int l = 2*i + 1; // left = 2*i + 1 
int r = 2*i + 2; // right = 2*i + 2 

2*i + 1 是 i的左節點
2*i + 2 是 i的右節點

這三個數字 ，看誰最大 。

如果 最大的是i ，就不用調整 ，因為MaxHeap本來就要root 是這三者中最大的 。

如果是左節點，或右節點 比較大 ，就跟i交換 。

交換後 ， 代表 原本在i索引的地方 ，變成左節點或右節點 的值

代表 原本在 左節點或右節點 索引的地方 ，變成 i索引 的值

原本在 左節點或右節點 索引的地方 這邊 寫為 largest(三者中最大值) 索引 。

largest索引 要再繼續跑heapify 。因為不確定largest 索引 是不是root ，如果是root ，還要繼續 跟左右節點 比誰大 。

看完heapify 後 ，來看主程式sort :

步驟是:

建Max Heap
去root
建Max Heap
去root
建Max Heap
去root

一開始建MaxHeap ，就是把每個parent節點，去跑heapify ，確保每個parent節點都是三者之中最大值 。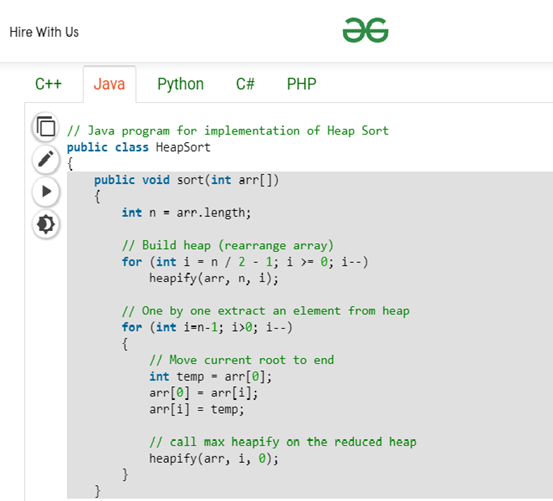

        // Build heap (rearrange array) 
        for (int i = n / 2 - 1; i >= 0; i--) 
            heapify(arr, n, i); 

如圖，索引有0到4
所以i 是 4/2-1 = 1
先檢查索引1底下是不是MaxHeap 。再檢查索引0底下是不是 MaxHeap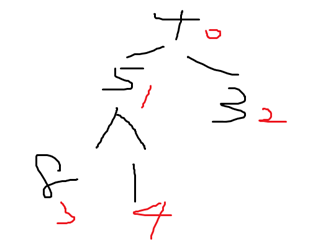

MaxHeap 還有另一種建立方法

如果數列12345678 ， 就從1 ，1、2， 1、2、3 ，這樣一個一個加入MaxHeap ，每加入一個數字，那個數字就要不斷往上跟root 比，改成MaxHeap ，時間複雜度是 n * logn
m 代表有幾個節點
log n 代表 往上比

如圖，4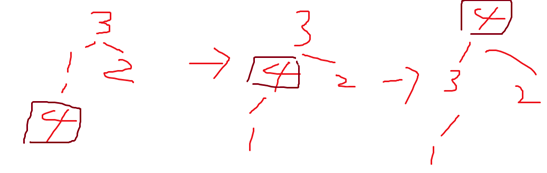

參考:
Why is the top down approach of heap construction less efficient than bottom up even though its order of growth is lower O(log n) over O(n)?
https://stackoverflow.com/questions/36226714/why-is-the-top-down-approach-of-heap-construction-less-efficient-than-bottom-up

這種方法是top down(root往下) ，程式裡的是bottom up(根往上)

程式裡的建立MaxHeap的時間複雜度是 Ο(n)

       // Build heap (rearrange array) 
        for (int i = n / 2 - 1; i >= 0; i--) 
            heapify(arr, n, i); 

直覺記法(錯誤記法?):因為從 最後一個parent節點 ，不斷往上面的parent跑 。
每個節點 大概走過一次 ，所以是 n 。

看這部教學:
Algorithms lecture 13-- Build max heap algorithm and analysis
https://www.youtube.com/watch?v=HI97KDV23Ig&ab_channel=GateLecturesbyRavindrababuRavula

這樣的想法應該不太正確:

直覺記法:因為從 最後一個parent節點 ，不斷往上面的parent跑 。
每個節點 大概走過一次 ，所以是 n 。

教學裡的解答是 :

高度0 -- >葉子 的heapify ，不用執行 ，時間複雜度O(0)

高度1-- >heapify 1層，時間複雜度O(1)

高度2 -- > heapify 2層，時間複雜度O(2)

高度3 -- > heapify 3層，時間複雜度O(3)

高度logn - > heapify  logn層，時間複雜度O(logn)

時間複雜度 : 每一層的節點個數 * heapify  的總和 。

總之最後結果是 O(n) ，看不懂證明 。

時間複雜度

建立MaxHeap： Ο(n)
執行n-1次Delete Max：(n-1) × Ο(log n) = Ο( n log n)
Ο(n) + Ο( n log n) = Ο( n log n)

因為 執行n-1次Delete Max時間複雜度 > MaxHeap時間複雜度
所以取Ο( n log n)

穩定性(Stable/Unstable)：不穩定(Unstable)

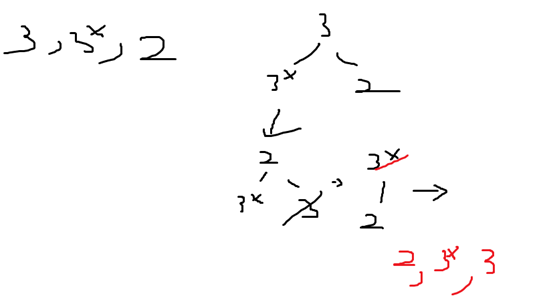
文章有說HeapSort也可以改成stable